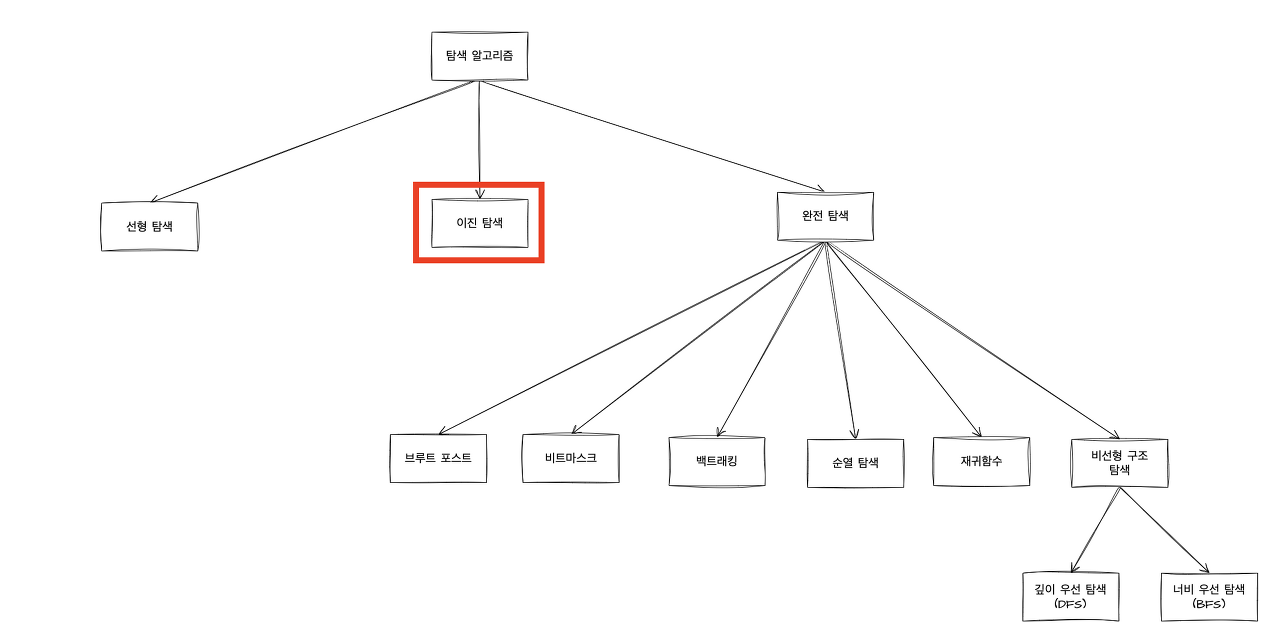
[Java] 이진탐색(Binary Search) 이란?

• 참고사이트
  • 블로그
• 자료구조와 알고리즘
  • 재귀함수
  • 선형탐색
  • 이진탐색
  • 완전탐색 #1 정의 및 종류
  • 완전탐색 #2 종류별설명
  • 완전탐색 #3 예시

이진 탐색(Binary Search) 이란?

• ‘정렬된 배열’에서 ‘특정 값’을 찾는 알고리즘을 의미

이진탐색은 탐색 범위를 절반씩 줄여나가기 때문에 선형탐색에 비해 빠른 속도를 보장한다. 하지만 배열이 정렬되어 있어야 한다는 조건이 필요하기 때문에 배열이 정렬되어 있지 않은 경우에는 정렬 작업이 필요하다.

선형 탐색(Linear Search) 이란?

배열이나 리스트의 처음부터 끝까지 하나씩 값을 비교하면서 찾는 값을 찾을 때까지 탐색하는 방법

선형 탐색의 경우 '정렬이 되지 않은 상태'의 배열/리스트에서 값을 찾기 위한 탐색에 사용합니다.
( 이진 탐색과 비교가 되며 정렬이 된 상태에서 사용하는 이진 탐색과 사용되는 방식이 다릅니다)

선형 탐색 동작 과정

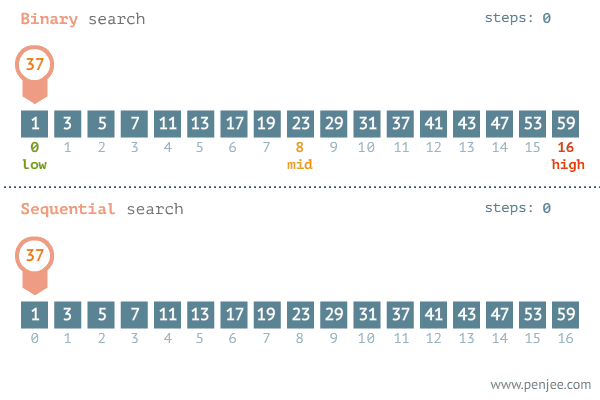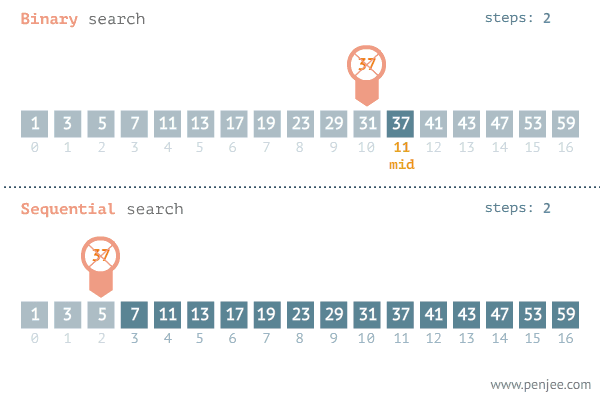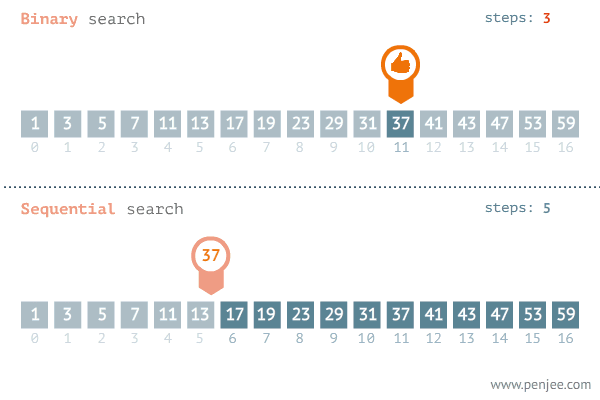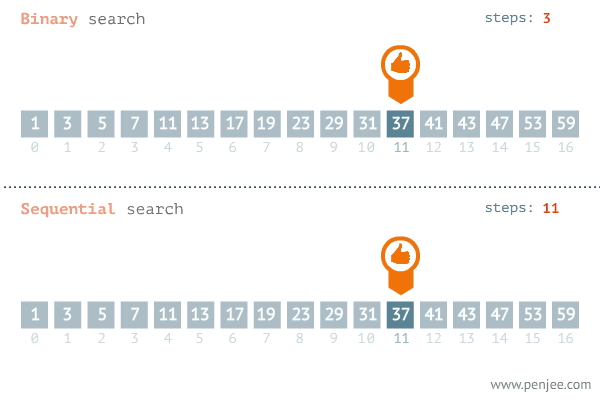
1. 배열의 ‘중간 값’을 선택하여 찾고자 하는 값과 비교한다.
2. 만약 중간 값이 찾고자 하는 값보다 크면 '배열 왼쪽 부분'에서 탐색을 진행하고, 값보다 작으면 '배열 오른쪽 부분'에서 탐색을 진행한다.
3. 이 과정하게 찾고자 하는 값이 나올 때까지 반복한다.

이진 탐색과 선형 탐색의 차이점

• 일반적으로 특정 값을 탐색하고자 할 때 값을 찾는 방법은 ‘이진 탐색’을 이용하는 것이 ‘for문’을 이용하는 것보다 보다 더 빠르다.

• 이진 탐색은 정렬 배열에서 원하는 값을 찾는 알고리즘이며, 중간값을 찾아 탐색 범위를 반으로 줄이면서 값을 찾아간다.

• 이에 비해 선형 탐색은 배열 전체를 순회하면서 값을 찾기 때문에 배열의 크기와 상관없이 속도가 일정하게 증가한다.

이진 탐색과 선형 탐색의 차이점

분류	선형 탐색(Linear Search)	이진 탐색(Binary Search)
정렬여부	정렬되지 않은 배열/리스트	정렬된 배열/리스트
탐색속도	느림	빠름
탐색범위	처음부터 끝까지	중간값ㅇ르 기준으로 좌/우측 반 중 하나
구현방식	for/while 루프 사용	재귀함수 사용
시간복잡도	O(n)	O(log n)

이진 탐색의 사용처

• 이진 탐색은 데이터가 오름차순으로 정렬되어 있을 때, 특정한 값을 찾아야 할 떄 사용한다.
• 데이터의 양이 많을 경우에도 빠른 시간 내에 값을 찾을 수 있어 많이 활용된다.

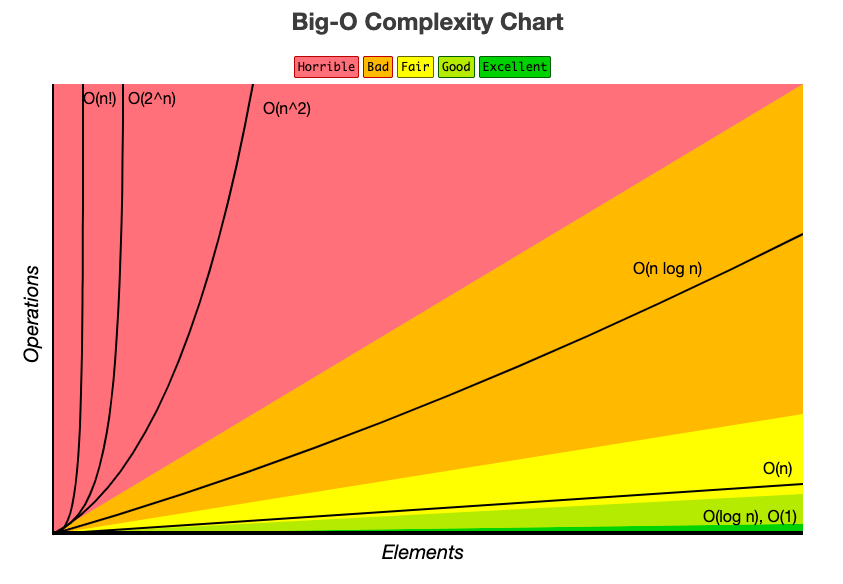
이진 탐색의 성능

💡 시간 복잡도(Time Complexity)란?

• 알고리즘이 실행될 때 필요한 ‘입력 값’과 ‘연산 수행 시간’에 따라 효율적인 알고리즘을 나타내는 척도를 의미합니다.

이진 탐색의 경우 시간 복잡도의 ‘빅오 표기법’을 이용하여 확인 하였을때 로그 시간인 O(log n) 으로써 다른 정렬에 비해 상대적으로 매우 빠르다.

표기법	이름	시간복잡도	설명	예시
O(1)	상수	상수 시간	입력 크기와 상관없이 일정한 실행 시간을 가진다.	배열에서 원소 하나 찾기
O(logn)	로그	로그 시간	입력 크기가 증가함에 따라 실행 시간이 로그함수의 형태로 증가한다	이진 탐색 알고리즘
O(n)	선형	선형 시간	입력 크기와 비례하는 실행 시간을 가진다	선형 탐색 알고리즘
O(nlogn)	로그 선형	선형 로그 시간	입력 크기가 증가함에 따라 실행 시간이 로그함수와 선형 함수의 곱의 형태로 증가한다	병합 정렬, 힙 정렬 알고리즘
O(n^2)	이차	이차 시간	입력 크기의 제곱에 비례하는 실행 시간을 가진다	선택 정렬, 버블 정렬, 퀵 정렬 알고리즘
O(2^n)	지수	지수 시간	입력 크기의 지수에 비례하는 실행 시간을 가진다	부분집합
O(n!)	계승	팩토리얼 시간	입력 크기의 팩토리얼에 비례하는 실행 시간을 가진다	외판원 문제

[참고] 이진 탐색과 비슷한 탐색을 비교 해보아도 시간 복잡도의 정도는 상대적으로 빠른것을 확인 할 수 있다.

알고리즘명	시간복잡도
선형 탐색	O(n)
이진 탐색	O(log n)
보간 탐색	O(log(log n))
해시 탐색	O(1)
깊이 우선 탐색	O(V + E)

이진 탐색의 숫자 탐색

배열 내의 숫자를 찾는 예시

• 해당 코드는 이진탐색의 예시를 보여준다.
• 예시는 int[] arr = {1, 3, 5, 8, 11, 15, 30, 32, 45}이고 key 값이 8인 경우의 이진탐색을 찾는 원리를 확인한다.

1. while 문으로 구성하는 이진 탐색

💡 아래의 예시는 정렬된 배열 arr에서 key 값을 찾는 이진 탐색을 구현한 예시이다.

• low는 첫번째 인덱스, high는 마지막 인덱스를 지정한다.
• 마지막 인덱스 보다 첫번째 인덱스가 같아지거나 작을 경우까지 순회한다.
• 중간 값을 구한다.
• 중간 값보다 찾으려는 값(key)가 큰 경우 중간 값에 1을 더하여 오른쪽 절반을 탐색한다.
• 중간 값보다 찾으려는 값(key)가 작은 경우 중간 값에 1을 빼고 왼쪽 절반만 탐색한다.
• 이외에 경우 중간 값을 최종값으로 반환한다.
• 최종 탐색을 못한 경우 값은 -1로 반환한다.

public static int binarySearch() {
    int[] arr = {1, 3, 5, 8, 11, 15, 30, 32, 45}; // 전체 배열
    int key = 8; // 찾고자 하는 요소
    int answer = 0;

    // 시작 인덱스와 마지막 인덱스 값을 지정
    int low = 0;
    int high = arr.length - 1;

    // 마지막 인덱스를 보다 첫번째 인덱스가 같아지거나 작을 경우까지 순회
    while (low <= high) {

        // 중간 값을 구한다.
        int mid = (low + high) / 2;

        // 중간 값보다 찾으려는 값(key)가 큰 경우 : 중간 값에 1을 더하여 오른쪽 절반을 탐색합니다.
        if (arr[mid] < key) {
            low = mid + 1;
        }
        // 중간 값보다 찾으려는 값(key)가 작은 경우 : 중간값에 1을 빼서 왼쪽 절반을 탐색합니다.
        else if (arr[mid] > key) {
            high = mid - 1;
        }
        // 해당 경우가 아니면 중간값을 최종 값으로 반환합니다.
        else {
            answer = mid;
        }
    }

    // 최종 탐색을 하지 못할 경우 -1을 반환
    if (answer == 0) answer = -1;

    return answer;
}

재귀 함수를 이용한 이진 탐색

• 높은 인덱스가 낮은 인덱스보다 크거나 같은지 확인한다.
• 중간 값을 구한다.
• 배열의 요소 값이 찾는 값과 동일하면 중간 값을 반환한다.
• 중간 값이 키보다 큰 경우 : 낮은 인덱스와 중간 인덱스에서 1을 뺀 값을 가지고 함수를 재귀적으로 호출한다.
• 중간 값이 키보다 작은 경우 : 중간 인덱스에 1을 더하고 높은 인덱스와 함께 함수를 재귀적으로 호출한다

/**
 * 재귀를 사용하여 이진 알고리즘을 구현
 * @param arr 배열
 * @param low 낮은 인덱스
 * @param high 높은 인덱스
 * @param key 검색할 값
 * @return
 */
public static int binarySearch(int[] arr, int low, int high, int key) {
    // 높은 인덱스가 낮은 인덱스보다 크거나 같은지 확인
    if (high >= low) {

        // 중간 값을 구한다
        int mid = low + (high - low) / 2;

        // 배열의 요소 값이 찾는 값과 동일하면 중간 값을 반환
        if (arr[mid] == key) {
            return mid;
        }
        // 중간 값이 키보다 큰 경우 : 낮은 인덱스와 중간 인덱스에서 1을 뺀 값을 가지고 함수를 재귀적으로 호출
        else if (arr[mid] > key) {
            return binarySearch(arr, low, mid - 1, key);
        }
        // 중간 값이 키보다 작은 경우 : 중간 인덱스에 1을 더하고 높은 인덱스와 함께 함수를 재귀적으로 호출
        else {
            return binarySearch(arr, mid + 1, high, key);
        }
    }

    // 높은 인덱스가 낮은 인덱스보다 작으면 배열에서 키를 찾지 못했음을 나타내기 위해 -1을 반환
    return -1;
}

이진 탐색의 문자열 탐색

• 문자열 배열의 경우 이진/이분 탐색을 사용하는 경우 Arrays.binarySarch() 함수를 이용한다.

Arrays.binarySearch()

💡 Arrays.binarySearch() 함수

• 매개변수로 주어진 배열에서 원하는 값을 이진 탐색하여 인덱스를 반환한다. 만약 해당 원소가 배열에 없다면 음수를 반환한다. 이진 탐색을 하기 전에 반드시 배열을 정렬해야 한다.

public static int binarySearch(Object[] a, Object key)

Arrays.binarySearch() 의 매개변수

타입	설명
Object[]	탐색하고자 하는 배열
Object	배열에서 찾으려는 값

Arrays.binarySearch()를 이용한 이진 탐색 예시

💡 해당 예시는 String[] 내에서 key 값을 찾고 있다. 💡 Arrays.binaraySearch() 함수를 이용하여 배열 내에 key 값이 존재하는지 확인.

import java.util.Arrays;

public static void binarySearch() {
    String[] arr = new String[]{"가", "나", "다", "라", "마", "바", "사"};
    String key = "라";

    Arrays.sort(arr);
    int result = Arrays.binarySearch(arr, key);
    if (result < 0) {
        System.out.println("Element is not present in the array.");
    } else {
        System.out.println("Element is present at index " + result);
    }
}