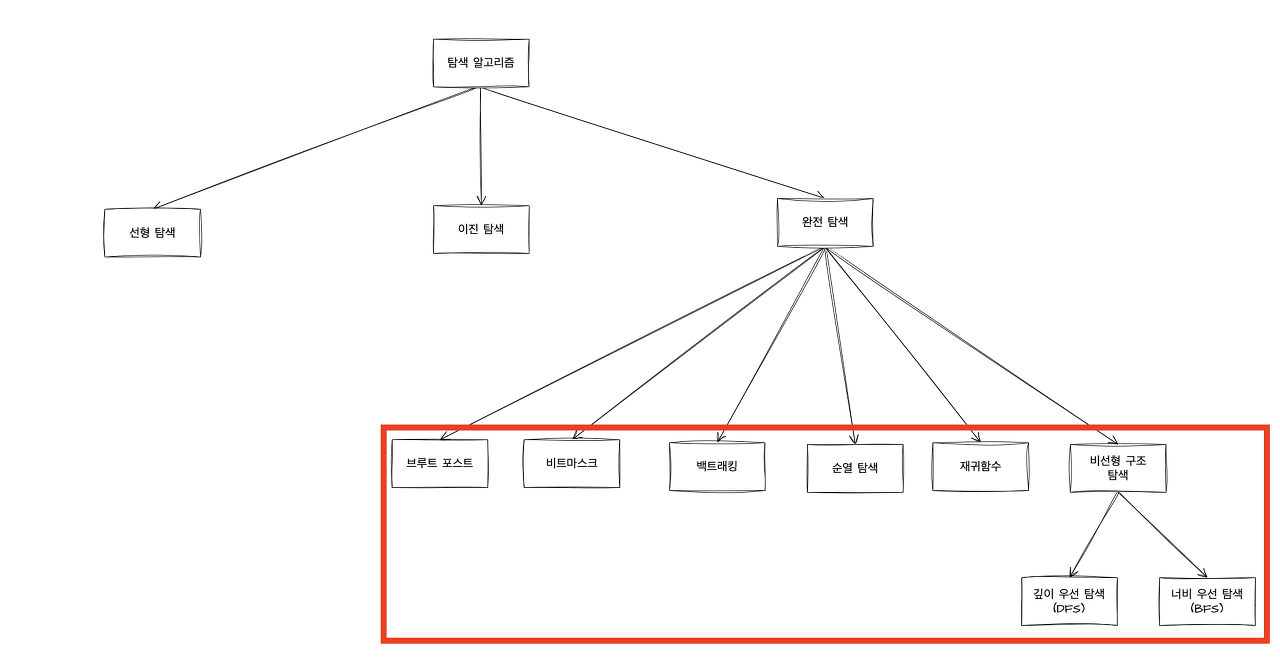
[Java] 완전탐색(Exhaustive Search) 이란? #1 정의 및 종류

• 참고사이트
  • 블로그
• 자료구조와 알고리즘
  • 재귀함수
  • 선형탐색
  • 이진탐색
  • 완전탐색 #1 정의 및 종류
  • 완전탐색 #2 종류별설명
  • 완전탐색 #3 예시

완전 탐색(Exhaustive Search) 이란?

• 알고리즘에서 사용되는 기법 중 하나로 ‘모든 가능한 경우의 수를 탐색’하여 ‘최적의 결과를 찾는 방법’을 의미

모든 가능성을 고려하기 때문에 항상 최적의 해를 찾을 수 있지만 경우의 수가 매우 많은 경우 시간과 메모리의 부담이 커질 수 있다. 그렇기에 문제의 특성에 따라 다른 탐색 기법을 사용하는 것이 좋다.

💡 미 완전 탐색은 무엇일까?

• 모든 경우의 수를 고려하지 하지 않고 더 이상 탐색이 필요 없는 경우 그 루트를 끊어버리는 것을 의미

• 예를 들어서 재귀함수가 함수를 모든 경우의 수를 탐색하다가 결과를 찾아서 탐색을 중지하는 경우 루트를 끊는 경우를 가지치기(Pruning)라고 한다. 이를 수행하면 불필요한 탐색을 줄일 수 있다.

완전 탐색의 종류

종류	설명	장점	단점
브루트 포스	‘모든 경우의 수를 탐색’하면서 원하는 결과를 얻는 알고리즘을 의미한다	가능한 모든 경우를 다 검사하기 때문에 예상된 결과를 얻을 수 있음	경우의 수가 많을 경우 시간이 오래 걸림
비트마스크	‘모든 경우의 수’를 이진수료 표현하고 ‘비트 연산’을 통해 원하는 결과를 빠르게 얻는 알고리즘을 의미	이진수 연산을 이용하여 계산 속도가 빠름	경우의 수가 많아질수록 메모리 사용량이 늘어남
백트래킹	결과를 얻기 위해 진행하는 도중에 ‘막히게 되면’ 그 지점으로 다시 돌아가서 ‘다른 경로를 탐색’하는 방식을 의미, 결국 모든 가능한 경우의 수를 탐색하여 해결책을 찾음	경우의 수를 줄이면서도 모든 경우를 탐색할 수 있음	재귀 함수를 이용하기 때문에 스택 오버플로우가 발생할 가능성 있음
순열	‘순열’을 이용하여 모든 경우의 수를 탐색하는 방법이다. 순열은 서로 다른 n개 중에서 r개를 선택하여 나열하는 방법을 의미	경우의 수가 적을 때 사용하면 유용함	경우의 수가 많을 경우 시간이 오래 걸림
재귀함수	자기 자신을 호출하여 모든 가능한 경우의 수를 체크하면서 최적의 해답을 얻는 방식을 의미	코드가 간결하며, 이해하기 쉬움	스택 오버플로우가 발생할 가능성이 있음
DFS/BFS	깊이 우선 탐색(DFS: Depth-First Search) - 루트 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법을 의미 너비 우선 탐색(Breadth-First Search: BFS) - 루트 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방법을 의미	미로 찾기 등에 유용함	최악의 경우, 모든 노드를 다 방문해야 하므로 시간이 오래 걸림

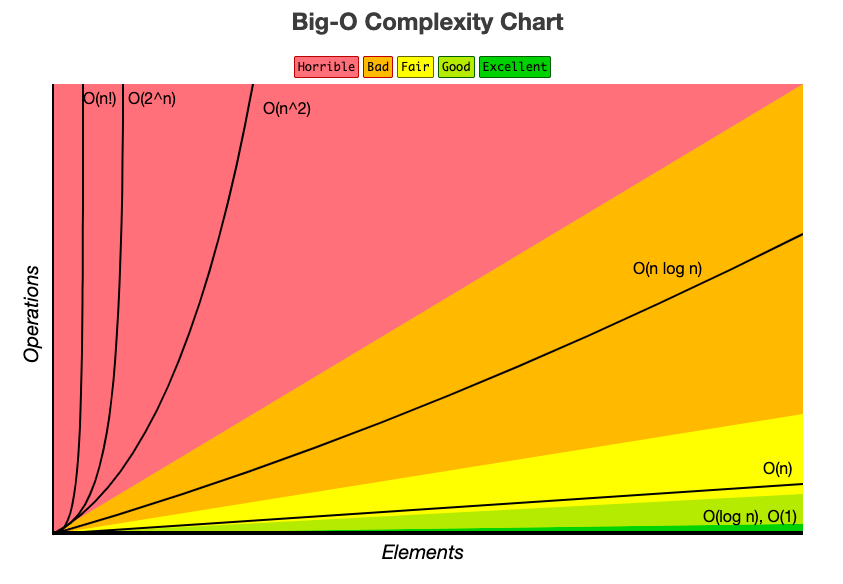
완전 탐색의 시간 복잡도

💡 시간 복잡도(Time Complexity)란?

• 알고리즘이 실행될 때 필요한 ‘입력 값’과 ‘연산 수행 시간’에 따라 효율적인 알고리즘을 나타내는 척도를 의미

표기법	이름	시간복잡도	설명	예시
O(1)	상수	상수 시간	입력 크기와 상관없이 일정한 실행 시간을 가진다.	배열에서 원소 하나 찾기
O(logn)	로그	로그 시간	입력 크기가 증가함에 따라 실행 시간이 로그함수의 형태로 증가한다	이진 탐색 알고리즘
O(n)	선형	선형 시간	입력 크기와 비례하는 실행 시간을 가진다	선형 탐색 알고리즘
O(nlogn)	로그 선형	선형 로그 시간	입력 크기가 증가함에 따라 실행 시간이 로그함수와 선형 함수의 곱의 형태로 증가한다	병합 정렬, 힙 정렬 알고리즘
O(n^2)	이차	이차 시간	입력 크기의 제곱에 비례하는 실행 시간을 가진다	선택 정렬, 버블 정렬, 퀵 정렬 알고리즘
O(2^n)	지수	지수 시간	입력 크기의 지수에 비례하는 실행 시간을 가진다	부분집합
O(n!)	계승	팩토리얼 시간	입력 크기의 팩토리얼에 비례하는 실행 시간을 가진다	외판원 문제

알고리즘명	시간복잡도
브루트 포스	O(nm)
비트마스크	O(2^n * n)
백트래킹	최악의 경우, O(n!)
순열	O(n!)
재귀함수	O(n)
DFS/BFS	O(V+E)