[Java] 완전탐색(Exhaustive Search) 이란? #2 종류별설명

November 6, 2023

참고사이트
- 블로그
자료구조와 알고리즘

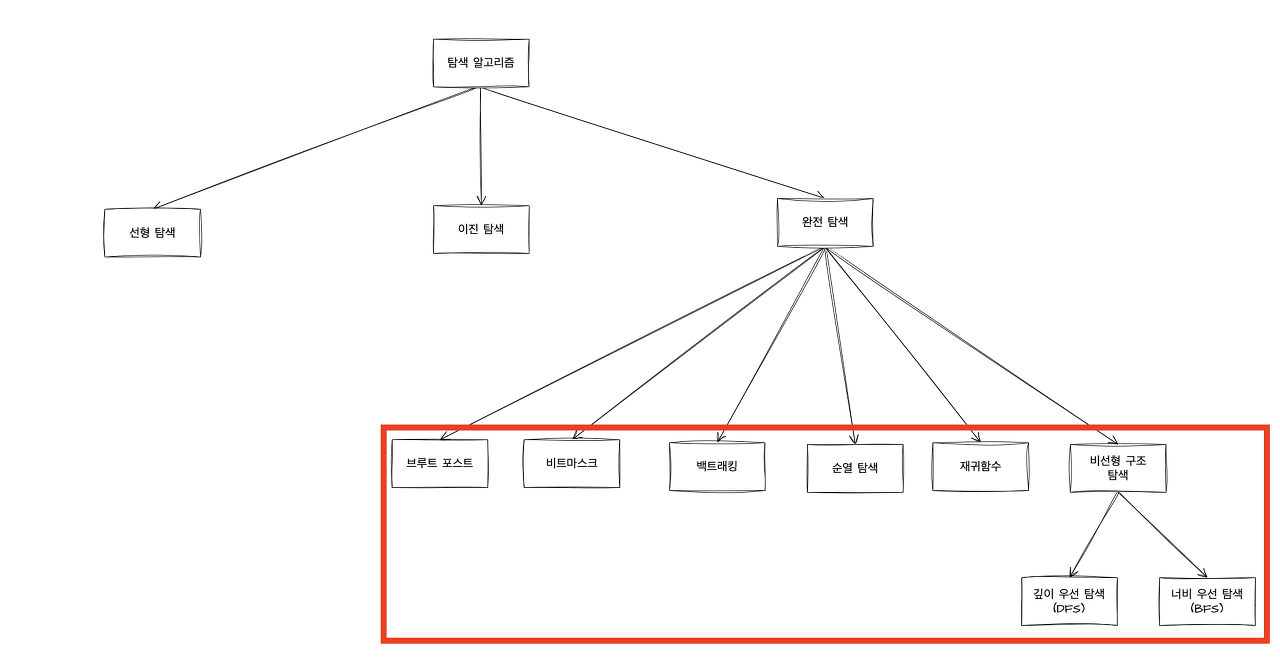
Algorithm

완전 탐색(Exhaustive Search) 이란?

알고리즘에서 사용되는 기법 중 하나로 모든 가능한 경우의 수를 탐색하여 최적의 결과를 찾는 방법`을 의미

모든 가능성을 고려하기 때문에 항상 최적의 해를 찾을 수 있지만 경우의 수가 매우 많은 경우 시간과 메모리의 부담이 커질 수 있다. 그렇기에 문제의 특성에 따라 다른 탐색 기법을 사용하는 것이 좋다.

브루트 포스(Brute-Force)

💡 브루트 포스(Brute-Force) 이란?

모든 경우를 다 탐색하면서 결과를 얻는 알고리즘을 의미
해당 알고리즘은 경우의 수가 작을 때 사용하는 것이 일반적이다. 대표적인 예시로는 자물쇠의 비밀번호를 알 수 없는 경우 모든 경우를 대입하여서 비밀번호를 찾아가는 경우가 있다.

💡 브루트 포스(Brute-Force)의 의미

영어로 부르트 포스는 “난폭한 힘, 폭력”이라는 뜻을 의미하며 무식하지만 확실한 방식을 의미한다. 이는 수행하는데 오래 걸리는 데다 자원이 많이 소요되지만 이론적으로 가능한 수를 모두 검색하기에 예상된 결과를 얻을 수 있다.

💡 완전 탐색에서 브루트 포스란?

모든 경우의 수를 탐색하여 최적의 결과를 찾아가는 완전탐색에서 브루트 포스는 모든 경우를 다 검사하여 원하는 값을 탐색하는 방법이다.

💡 브루트 포스를 이용한 공격방식이란?

해커들은 이 알고리즘을 이용하여 다양한 공격을 시도한다. 예를 들어, 로그인 페이지에서 사용자 이름과 비밀번호를 입력하여 로그인하는 경우 해커들은 브루트 포스 알고리즘을 이용하여 가능한 모든 비밀번호를 시도하면서 로그인을 시도한다. 이러한 공격을 방지하기 위해서는 강력한 비밀번호를 사용하고 로그인 시도 횟수를 제안하는 등의 보안 조치를 취해야 한다.

브루토 포스 사용 예시

배열탐색

💡 배열에서 특정 값을 찾는 문제에서 브루트 포스 알고리즘은 배열을 모두 탐색하여 값을 찾는 방식으로 문제를 해결합니다.

public static int findIndex(int[] arr, int target) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

문자열 비교

💡 문자열 비교 문제에서 브루트 포스 알고리즘은 가능한 모든 문자열 쌍을 비교하여 최소값 또는 최대값을 찾는 방식으로 문제를 해결합니다.

public static int stringCompare(String s1, String s2) {
    int n1 = s1.length(), n2 = s2.length();
    int min = Math.min(n1, n2);

    for (int i = 0; i < min; i++) {
        if (s1.charAt(i) != s2.charAt(i)) {
            return s1.charAt(i) - s2.charAt(i);
        }
    }

    if (n1 == n2) {
        return 0;
    } else if (n1 > n2) {
        return s1.charAt(min);
    } else {
        return s2.charAt(min);
    }
}

비트마스크

💡 비트마스크(bitmask)란?

이진수를 비트 연산을 통해 경우의 수를 줄여가며 탐색하는 방식을 의미
비트 마스크를 사용하면 하나의 변수에 여러 개의 상태 정보를 저장할 수 있으며 이를 통해 복잡한 조건문을 간단하게 처리할 수 있다. 이 방법은 비트 연산을 사용하기 때문에 빠르게 계산할 수 있어서, 경우의 수가 많은 경우에 유용하다.

💡 이진수란?

0과 1로 이루어진 수의 체계를 의미합니다.

💡 이진법이란?

이진수를 사용하여 숫자를 표현하는 방법을 의미합니다.

💡 완전 탐색에서 비트마스크란?

모든 경우의 수를 탐색하여 최적의 결과를 찾아가는 완전탐색에서 비트마스크는 모든 경우의 수를 이진수로 표현하여 빠르게 계산을 해 나아가는 방식입니다.

비트마스크의 비트연산

연산자	설명
&	두 비트 모두 1일 때 1을 반환, 그 외에는 0을 반환
\|	두 비트 중 하나라도 1일 때 1을 반환, 둘 다 0일 때 0을 반환
^	두 비트가 다를 때 1을 반환, 같을 때 0을 반환
~	비트를 반전시켜 반환
«	비트를 왼쪽으로 이동
»	비트를 오른쪽으로 이동

비트마스크의 이진수 연산의 예시

int a = 10; // 1010
int b = 12; // 1100

int result1 = a & b; // 1000
int result2 = a | b; // 1110
int result3 = a ^ b; // 0110
int result4 = a << 1; // 10100
int result5 = a >> 1; // 0101

비트마스크 사용 예시

권한관리

💡 보통 권한은 4가지 이상으로 구분되어 있는 경우가 많습니다. 이때 각 권한을 비트로 표현하여 하나의 정수값으로 나타내면 매우 간편해진다.

public static final int PERMISSION_READ = 1 << 0; // 0001
public static final int PERMISSION_WRITE = 1 << 1; // 0010
public static final int PERMISSION_DELETE = 1 << 2; // 0100
public static final int PERMISSION_EXECUTE = 1 << 3; // 1000

int userPermission = PERMISSION_READ | PERMISSION_WRITE; // 0011
int groupPermission = PERMISSION_READ | PERMISSION_EXECUTE; // 1001

boolean hasReadPermission = (userPermission & PERMISSION_READ) != 0; // true
boolean hasDeletePermission = (groupPermission & PERMISSION_DELETE) != 0; // false

집합관리

💡 집합을 비트로 표현하여 메모리를 절약할 수 있습니다. 예를 들어, 0부터 31까지의 정수 중에서 3, 5, 7번째 원소를 포함하는 집합을 나타내면 다음과 같이 표현할 수 있습니다.

int set = (1 << 3) | (1 << 5) | (1 << 7); // 0010 1010 1000

boolean hasElement5 = (set & (1 << 5)) != 0; // true
boolean hasElement6 = (set & (1 << 6)) != 0; // false

상태 플래그 관리

💡 여러 상태를 하나의 정수 값으로 나타내어 관리할 수 있습니다. 예를 들어, 주어진 수가 2의 거듭제곱인지 여부를 판단할 때 다음과 같은 방법을 사용할 수 있습니다.

public static final int FLAG_POWER_OF_TWO = 1 << 0; // 0001
public static final int FLAG_NEGATIVE = 1 << 1; // 0010

int number = 8; // 2의 거듭제곱
int flags = 0;

if ((number & (number - 1)) == 0) { // 2의 거듭제곱인 경우
    flags |= FLAG_POWER_OF_TWO;
}

if (number < 0) { // 음수인 경우
    flags |= FLAG_NEGATIVE;
}

if ((flags & FLAG_POWER_OF_TWO) != 0) {
    System.out.println(number + " is power of two");
}

if ((flags & FLAG_NEGATIVE) != 0) {
    System.out.println(number + " is negative");
}

백트래킹(Backtracking)

💡 백트래킹(Backtracking)

해결책으로 가는 도중에 막히게 되면 그 지점으로 다시 돌아가서 다른 경로를 탐색하는 방식을 의미하나다. 이를 통해 모든 가능한 경우의 수를 탐색하여 해결책을 찾는다.
해당 알고리즘을 사용할때 주로 재귀함수를 사용하여 구현하며 스택을 이용하여서 사용하는 경우도 있다.
재귀함수를 이용하는 경우 해결책을 찾기 위해 생성, 검사, 선택, 이동, 되돌아가기 등 과정이 재귀적으로 수행된다.
스택을 이용하는 경우 이전 상태로 되돌아가기 위해 스택에 현재 상태를 저장하고, 되돌아갈 때 스택에서 상태를 꺼내오는 형태로 수행한다.

💡 완전 탐색에서 백트래킹이란?

모든 경우의 수를 탐색하여 최적의 결과를 찾아가는 완전탐색에서 백트래킹은 해결책을 찾아가는 도중에 막히게 되면 다시 돌아가서 다른 경로로 탐색을 하여 결국 모든 가능한 경우의 수를 탐색하여 해결책을 찾아가는 방식으로 사용됩니다.

순열탐색(Permutation Search)

💡 순열 탐색(Permutation Search) 이란?

순열을 이용하여 모든 경우의 수를 탐색하는 방법입니다. 순열은 서로 다른 n개 중에서 r개를 선택하여 숫자를 모든 순서대로 뽑는 경우를 말합니다.

💡 순열의 예

1, 2, 3 세 숫자 중에서 ‘2개를 선택’하여 숫자를 모든 순서대로 뽑는 경우입니다.

[1,2]
[1,3]
[2,1]
[2,3]
[3.1]

Swap 배열을 이용한 순열

💡 Swap 배열

배열에서 두 요소의 위치를 바꿔가며 순열을 생성하는 방법이다. 배열의 인덱스 0 부터 순서대로 선택하여 다음 인덱스와 위치를 바꾸고 이를 마지막 인덱스까지 반복한다.
이 방법은 쉽게 구현할 수 있지만, 큰 데이터셋에서는 비효율적일 수 있다.

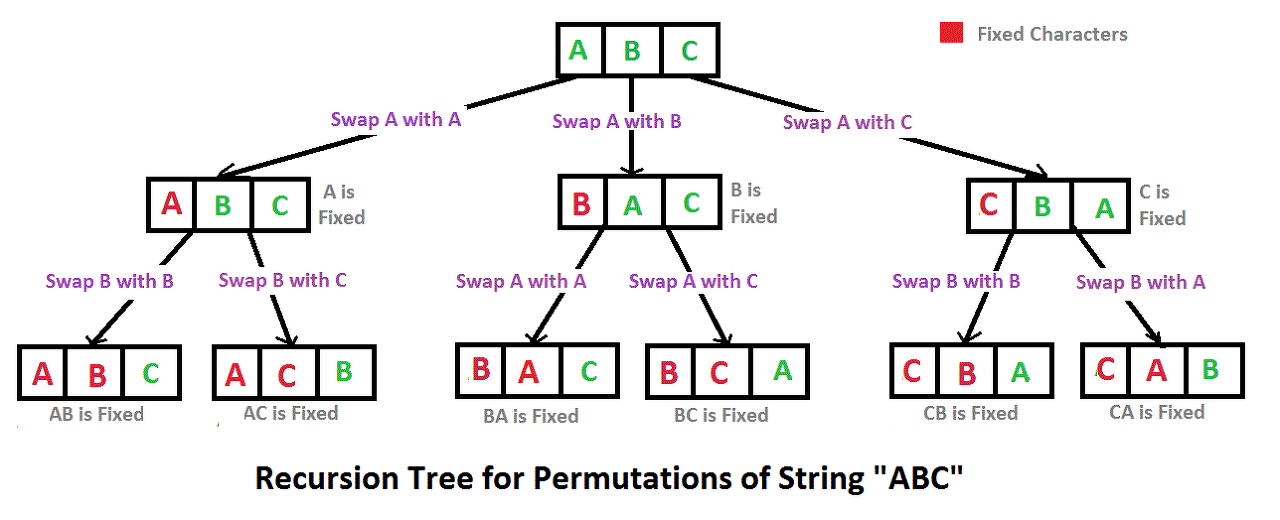
Algorithm

💡 [1, 2, 3] 배열에서 순열을 모두 구하는 예시

메인 함수에서 permute 메서드에 파라미터로 배열과 0개를 선택
permute 메서드는 재귀적으로 호출하며 swap 메서드를 이용하여 배열의 원소를 순서대로 바꾸면서 모든 순열을 생성
이때, k는 순열을 생성할 위치를 의미. 만약 k가 arr의 길이와 같아지면, 모든 원소에 대한 순열이 생성되었다는 것을 의미하므로 순열을 출력

import java.util.*;

public class Permutation {
    /**
     * 순열의 로직을 수행
     *
     * @param arr
     * @param k
     */
    static void permute(int[] arr, int k) {
        for (int i = k; i < arr.length; i++) {
            swap(arr, i, k);
            permute(arr, k + 1);
            swap(arr, k, i);
        }
        if (k == arr.length - 1) {
            System.out.println(Arrays.toString(arr));
        }
    }

    /**
     * 배열의 요소 값을 Swap
     *
     * @param arr
     * @param i
     * @param j
     */
    static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3};
        // 메인 함수에서 permute 메서드에 파라미터로 배열과 0개를 선택
        permute(arr, 0);
    }
}


// 출력
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 2, 1]
[3, 1, 2]

💡 완전 탐색에서 순열은?

모든 경우의 수를 탐색하여 최적의 결과를 찾아가는 완전탐색에서 순열은 서로 다른 n개 중에서 r개를 선택해서 나열하면서 모든 경우의 수를 탐색하는 방식으로 사용이 딘다.

💡 배열의 요소를 Swap 한다는 말은 무슨 말인가?

배열의 요소를 임시 공간에 두고 서로 요소의 위치를 바꾸는 것을 의미
예를 들면 A, B, C가 있는데 A와 C의 위치를 바꾼다고 하면 임시 변수를 만들어서 A를 임시공간에 두었다가 C를 A로 옮기고 A는 임시 변수의 값을 가져와서 바꾸는것을 의미

Visited 배열을 이용한 순열

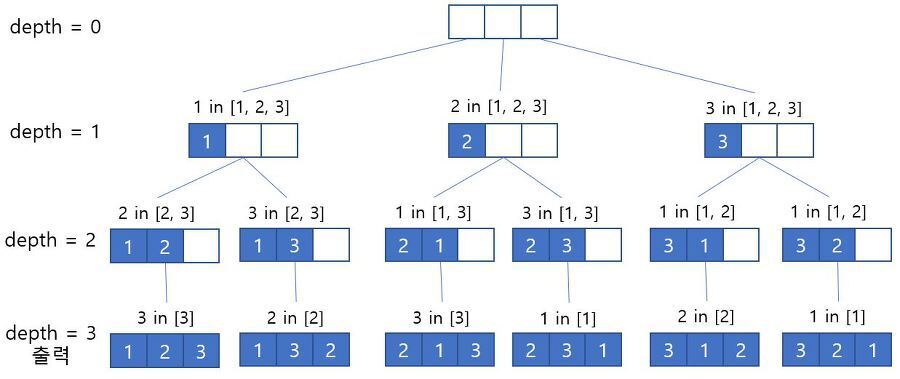
💡Visited 배열

배열에서 ‘현재 인덱스의 값을 선택한 후’ 해당 인덱스를 visited라는 배열에 체크
다음 인덱스로 넘어가기 전 visited 배열에서 체크되지 않은 가장 작은 인덱스를 선택
이를 마지막 인덱스까지 반복
이 방법은 swap을 이용한 배열보다 효율적이다.

Algorithm

public class Permutation {
    public static void main(String[] args) {
        int n = 3;
        int[] arr = {1, 2, 3};
        int[] output = new int[n];
        boolean[] visited = new boolean[n];

        perm(arr, output, visited, 0, n, 3);
			 // Swap 순열
       // System.out.println();
       // permutation(arr, 0, n, 3);
    }

    static void perm(int[] arr, int[] output, boolean[] visited, int depth, int n, int r) {
        if (depth == r) {// 3개가 되면 출력
            print(output, r);
            return;
        }

        for (int i = 0; i < n; i++) {
            if (visited[i] != true) {
                visited[i] = true;
					      // 숫자 선정 완료(체크)
                output[depth] = arr[i]; 
								// 출력할 숫자 선정
								// depth가 출력할 숫자의 위치
                perm(arr, output, visited, depth + 1, n, r); 
								// 재귀함수 호출
                visited[i] = false;     
								// 숫자 선정 취소
            }
        }
    }

    
    static void print(int[] arr, int r) {// 출력 메소드
        for (int i = 0; i < r; i++)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
}

재귀함수

💡 재귀 함수(Recursion Function)란?

함수 내부에서 자기 자신을 호출하는 함수를 의미
이를 통해서 함수가 자신을 반복적으로 호출하면서 원하는 결과를 도출할 수 있다.

💡 완전 탐색에서 재귀함수는?

모든 경우의 수를 탐색하여 최적의 결과를 찾아가는 완전탐색에서 재귀함수는 자기 자신을 호출하며 모든 가능한 경우를 체크하면서 최적의 해답하는 방법으로 사용이 됩니다.

💡 재귀함수는 미 완전 탐색일 수도 있다?

재귀함수는 모든 경우의 수를 다 탐색하지 않고도 원하는 결과를 얻을 수 있는 경우도 있습니다. 따라서, 재귀함수는 미완전탐색의 일종이라고는 할 수 있지만, 항상 미완전탐색이라고 할 수는 없습니다.

팩토리얼 계산 방법

💡 해당 기능은 factorial() 함수에 파라미터로 값을 넘길 경우 재귀함수로 반복하여 모든 경우의 수를 체크하여 결과값을 반환하는 함수이다.

public class Main {
    public static void main(String[] args) {
        System.out.println(factorial(5));// 5! = 5 * 4 * 3 * 2 * 1 = 120
    }

    public static int factorial(int n) {
        if (n == 0) {// 기본 케이스
            return 1;
        } else {// 재귀 케이스
            return n * factorial(n - 1);
        }
    }
}

N 자연수의 합 계산 방법

💡 해당 기능은 sumNaturalNumber() 함수에 파라미터로 값을 넘길 경우 재귀함수를 반복하여 모든 경우의 수를 체크하여 결과값을 반환하는 함수이다.

public class Main {
    public static void main(String[] args) {
        System.out.println(sumNaturalNumber(5));// 15
    }

    public static int sumNaturalNumber(int n) {
        if (n == 1) {
            return 1;
        } else {
            return n + sumNaturalNumber(n - 1);
        }
    }
}

거듭제곱(pow) 계산

💡 해당 기능은 거듭제곱으로 base, exponent 값을 파라미터로 받아서 모든 경우의 수를 체크하여 결과값을 반환하는 함수이다.

public class Main {
    public static void main(String[] args) {
        System.out.println(power(2, 5));// 15
    }

    public static int power(int base, int exponent) {
        if (exponent == 0) {
            return 1;
        } else {
            return base * power(base, exponent - 1);
        }
    }
}

깊이 우선 탐색(DFS: Depth-First Search)

💡 깊이 우선 탐색(DFS: Depth-First Search) 이란?

루트 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법을 의미
해당 방식은 자료구조의 스택을 이용하여서 구현할 수 있다
연결된 노드를 따라서 계속 방문을 한 후에 더 이상 연결된 노드들을 없을 때 그 전 노드로 되돌아가고 다시 연결된 노드를 따라서 탐색을 한다.

분류	깊이우선탐색(DFS)	너비우선탐색(BFS)
자료구조	스택	큐
탐색방식	깊이 우선	너비 우선
모든 경로 탐색	O	X
최단 경로 탐색	X	O
재귀 구현 가능	O	X
반복문 구현 가능	X	O
메모리 사용량	적음	많음

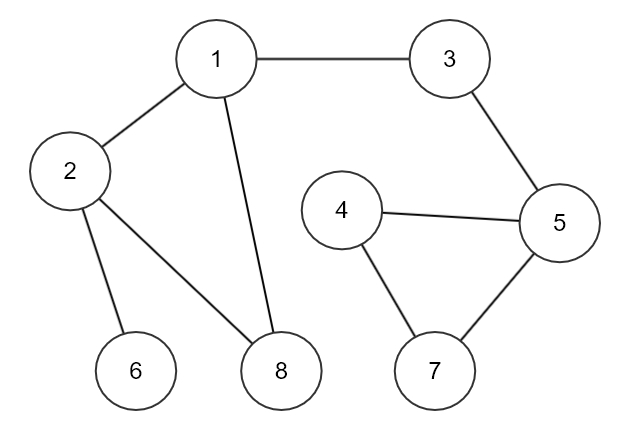
Algorithm

위와 같은 그래프가 존재한다고 하고, 1번 노드부터 DFS탐색을 해보자.

1번 노드 방문처리 후 출력 (탐색 순서 : 1)
1번 노드에 인접한 노드 2번, 3번, 8번 중 하나를 방문해야 하는데 오름차순으로 방문하기로 가정
2번 노드 방문처리 후 출력 (탐색 순서 : 1 -> 2)
2번 노드에 인접한 노드 6번, 8번 중 오름차순 기준이니까 6번 노드로 이동
6번 노드 방문처리 후 출력 (탐색 순서 : 1 -> 2 -> 6)
6번 노드에 인접한 노드는 2번 노드뿐인데 이미 방문을 하였으므로 더 이상 방문처리는 하지 않고 6번노드를 호출한 노드(부모 노드)로 다시 돌아간다. (여기서는 2번 노드)
2번 노드에 인접한 노드 중 8번 노드가 남아있으므로 8번 노드로 이동
8번 노드 방문처리 후 출력 (탐색 순서 : 1 -> 2 -> 6 -> 8)
8번 노드에 인접한 노드는 1번과 2번 노드인데 둘 다 모두 방문처리가 되어있으므로 더 이상 방문은 하지 않고 8번을 호출한 노드(부모 노드)인 2번 노드로 이동
2번 노드에 인접한 노드(자식 노드) 6번, 8번이 모두 방문 처리된 상태이므로 2번을 호출한 노드(부모 노드)인 1번 노드로 이동
이제 1번 노드에 인접한 노드 중 방문하지 않은 노드 3번으로 이동
3번 노드 방문처리 후 출력 (탐색 순서 : 1 -> 2 -> 6 -> 8 -> 3)
3번 노드에 연결된 노드는 5번 노드뿐이므로 5번 노드 방문 처리 후 출력 (탐색 순서 : 1 -> 2 -> 6 -> 8 -> 3 -> 5)
5번 노드에 연결된 노드 4번, 7번 중 오름차순 기준이니까 4번 먼저 방문처리 후 출력
마지막으로 남은 7번 노드 방문 처리 후 출력하면 더 이상 방문할 노드가 없으므로 종료

이렇게 되면 최종적으로 탐색한 순서는 다음과 같다.
탐색 순서(재귀) : 1 -> 2 -> 6 -> 8 -> 3 -> 5 -> 4 -> 7
저는 오름차순 기준으로 해서 위와 같은 탐색 순서가 나왔지만, 기준이나 구현 방법에 따라서 탐색 순서는 바뀔 수 있다.
DFS를 코드로 구현하는 방법은 재귀로 구현하는 방법과 Stack자료구조를 사용해서 구현하는 방법 2가지가 있다.
위의 설명 예시는 재귀 형태로 구현했을 때의 탐색 순서이다.
만약에 Stack자료구조로 구현을 한다면 연결된 자식 노드를 오름차순으로 Stack에 집어넣고 하나씩 꺼내서 다시 연결된 노드를 찾아서 Stack에 넣는 식으로 구현을 할 수 있다.
이러한 형태로 탐색은 진행하면 순서는 다음과 같다.
탐색 순서(Stack자료구조) : 1 -> 8 -> 3 -> 5 -> 7 -> 4 -> 2 -> 6
실제 코드로 구현해보면 스택 자료구조를 사용한 것보다는 재귀로 구현하는 게 코드가 더 짧고 간결하기 때문에 일반적으로 재귀로 많이 구현을 한다.

재귀함수로 구현

재귀함수를 이용해 구현하면 아래와 같다.

public class Main {
	
    public static void main(String[] args) {
        boolean[] vistied = new boolean[9];

        // 그림예시 그래프의 연결상태를 2차원 배열로 표현
        // 인덱스가 각각의 노드번호가 될 수 있게 
        // 0번인덱스는 아무것도 없는 상태라고 가정
        int[][] graph = { {}, {2,3,8}, {1,6,8}, {1,5}, {5,7}, {3,4,7}, {2}, {4,5}, {1,2} };
        // 방문처리에 사용 할 배열선언    
        depthFirstSearch(vistied, graph, 1);
    }

    public static void depthFirstSearch(boolean[] vistied, int[][] graph, int nodeIndex) {

        // 방문 처리
        vistied[nodeIndex] = true;

        // 방문 노드 출력
        System.out.print(nodeIndex + " -> ");

        // 방문한 노드에 인접한 노드 찾기
        for (int node : graph[nodeIndex]) {
            // 인접한 노드가 방문한 적이 없다면 DFS 수행
            if(!vistied[node]) {
                depthFirstSearch(vistied, graph, node);
            }
        }
    }
}

Stack 을 이용한 구현

public class Main {

	// 방문처리에 사용 할 배열선언
	static boolean[] vistied = new boolean[9];
	
	// 그림예시 그래프의 연결상태를 2차원 배열로 표현
	// 인덱스가 각각의 노드번호가 될 수 있게 0번인덱스는 아무것도 없는 상태라고 가정
	static int[][] graph = { {}, {2,3,8}, {1,6,8}, {1,5}, {5,7}, {3,4,7}, {2}, {4,5}, {1,2} };
	
	// DFS 사용 할 스택
	static Stack<Integer> stack = new Stack<>();
	
	public static void main(String[] args) {
		
		// 시작 노드를 스택에 넣는다
		stack.push(1);
		// 시작 노드 방문처리
		vistied[1] = true;
		
		// 스택이 비어있지 않으면 계속 반복
		while(!stack.isEmpty()) {
			
			// 스택에서 하나를 꺼낸다.
			int nodeIndex = stack.pop();
			
			// 방문 노드 출력
			System.out.print(nodeIndex + " -> ");
			
			// 꺼낸 노드와 인접한 노드 찾기
			for (int LinkedNode : graph[nodeIndex]) {
				// 인접한 노드를 방문하지 않았을 경우에 스택에 넣고 방문처리 
				if(!vistied[LinkedNode]) {
					stack.push(LinkedNode);
					vistied[LinkedNode] = true;
				}
			}
		}
	}
}

너비 우선 탐색(Breadth-First Search: BFS)

💡 너비 우선 탐색(Breadth-First Search: BFS) 이란?

루트 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방법을 의미
해당 방식은 자료구조의 ‘큐’를 이용하여서 구현할 수 있다
기본적으로 그래프 탐색에 사용되며, 가까운 노드부터 우선적으로 탐색하는 알고리즘

분류	깊이우선탐색(DFS)	너비우선탐색(BFS)
자료구조	스택	큐
탐색방식	깊이 우선	너비 우선
모든 경로 탐색	O	X
최단 경로 탐색	X	O
재귀 구현 가능	O	X
반복문 구현 가능	X	O
메모리 사용량	적음	많음

Algorithm

위와 같은 그래프가 존재하고 노드의 탐색은 1번부터 시작한다고 가정

큐에 1번 노드를 넣고 방문 처리 (여기서 방문처리라는 것은 내가 해당 노드에 방문했음을 기록하는 것)
1번 노드와 가까운 노드를 큐에 넣고 방문 처리합니다. (2번, 3번 8번 노드) (어떻게 넣어도 상관 없다. 오름차순으로 넣는다.)
큐에서 노드를 하나 꺼낸다.
연결된 노드가 없으면 3번으로 다시 돌아간다.
연결된 노드가 있고 방문하지 않았으면 큐에 넣고 방문처리 후 3번으로 돌아간다.
연결된 노드가 있지만 방문을 이미 한 경우에는 3번으로 돌아간다.
3~6을 큐가 빌 때까지 반복하며 큐가 비었으면 종료한다.
이러한 순서로 BFS를 진행하면 위의 그래프에서 탐색 순서는 다음과 같다.
1 -> 2 -> 3 -> 8 -> 6 -> 5 -> 4 -> 7
BFS알고리즘은 각 노드 간의 간선의 길이가 동일할 경우 최단거리를 구하는 알고리즘으로도 사용할 수 있다.

BFS 구현

public class Main {

	public static void main(String[] args) {
		
		// 그래프를 2차원 배열로 표현한다.
		// 배열의 인덱스를 노드와 매칭시켜서 사용하기 위해 인덱스 0은 아무것도 저장하지 않는다.
		// 1번인덱스는 1번노드를 뜻하고 노드의 배열의 값은 연결된 노드들이다.
        // {}, {1번노드와 연결된 노드}, {2번노드와 연결된 노드}, {3번노드와 연결된 노드}, {4번노드와 연결된 노드}, ...
		int[][] graph = { {}, {2,3,8}, {1,6,8}, {1,5}, {5,7}, {3,4,7}, {2}, {4,5}, {1,2} };
		
		// 방문처리를 위한 boolean배열 선언
		boolean[] visited = new boolean[9];
		
		System.out.println(bfs(1, graph, visited));
		//출력 내용 : 1 -> 2 -> 3 -> 8 -> 6 -> 5 -> 4 -> 7 -> 
	}
	
	static String bfs(int start, int[][] graph, boolean[] visited) {
		// 탐색 순서를 출력하기 위한 용도
		StringBuilder sb = new StringBuilder();
		// BFS에 사용할 큐를 생성
		Queue<Integer> q = new LinkedList<Integer>();
		 
		// 큐에 BFS를 시작 할 노드 번호를 넣는다
		q.offer(start);
		
		// 시작노드 방문처리
		visited[start] = true;
		
		// 큐가 빌 때까지 반복
		while(!q.isEmpty()) {
			int nodeIndex = q.poll();
			sb.append(nodeIndex + " -> ");
			//큐에서 꺼낸 노드와 연결된 노드들 체크
			for(int i=0; i<graph[nodeIndex].length; i++) {
				int temp = graph[nodeIndex][i];
				// 방문하지 않았으면 방문처리 후 큐에 넣기
				if(!visited[temp]) {
					visited[temp] = true;
					q.offer(temp);
				}
			}
		}
		// 탐색순서 리턴
		return sb.toString() ;
	}

    
}

Share on

Twitter Facebook LinkedIn

MyungKi You

[Java] 완전탐색(Exhaustive Search) 이란? #2 종류별설명

완전 탐색(Exhaustive Search) 이란?

브루트 포스(Brute-Force)

브루토 포스 사용 예시

비트마스크

비트마스크의 비트연산

비트마스크 사용 예시

백트래킹(Backtracking)

순열탐색(Permutation Search)

Swap 배열을 이용한 순열

Visited 배열을 이용한 순열

재귀함수

팩토리얼 계산 방법

N 자연수의 합 계산 방법

거듭제곱(pow) 계산

깊이 우선 탐색(DFS: Depth-First Search)

재귀함수로 구현

Stack 을 이용한 구현

너비 우선 탐색(Breadth-First Search: BFS)

BFS 구현

Share on

Leave a comment

You may also enjoy

[AWS] 프로젝트 자동 배포하기(CICD) EC2 & S3 & CodeDeploy

[AWS] VPC 설정하여 EC2 생성하기

[AWS] AWS VPC 설정하기

[React] Tree View 사용하기 (Typescript)