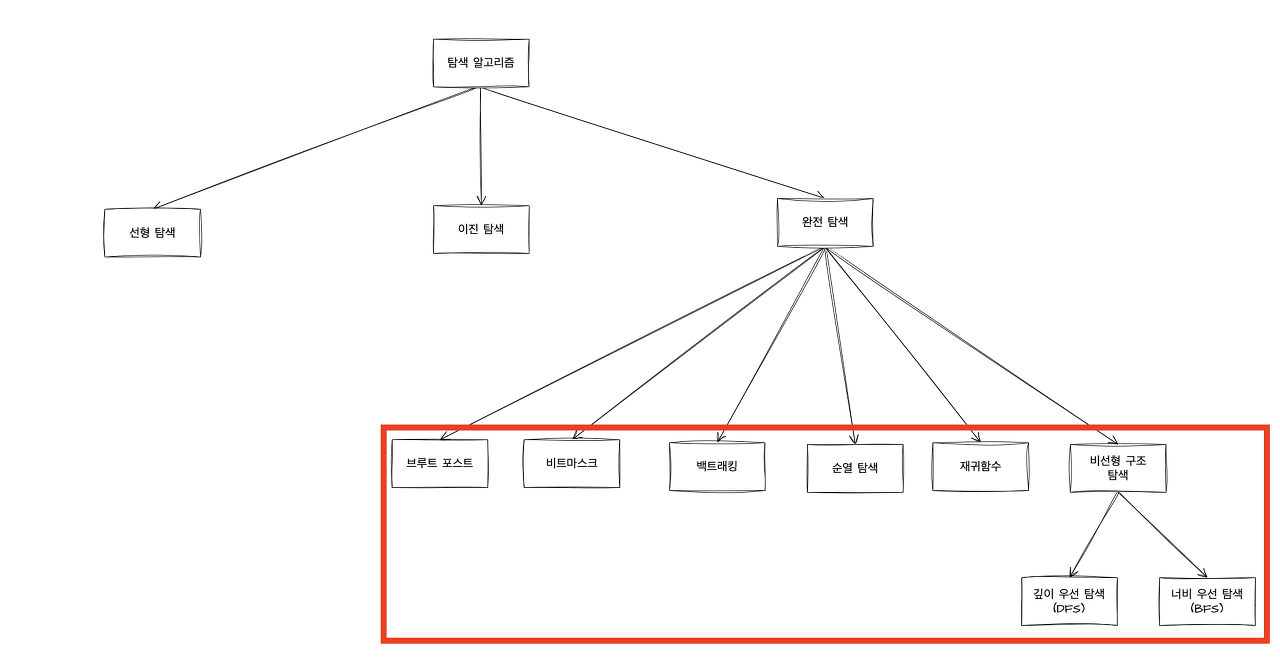
[Java] 완전탐색(Exhaustive Search) 이란? #3 예시
- 참고사이트
- 자료구조와 알고리즘
완전 탐색(Exhaustive Search) 이란?
- 알고리즘에서 사용되는 기법 중 하나로
모든 가능한 경우의 수를 탐색하여최적의 결과를 찾는 방법`을 의미
모든 가능성을 고려하기 때문에 항상 최적의 해를 찾을 수 있지만 경우의 수가 매우 많은 경우 시간과 메모리의 부담이 커질 수 있다. 그렇기에 문제의 특성에 따라 다른 탐색 기법을 사용하는 것이 좋다.
완전 탐색의 종류
| 종류 | 설명 | 장점 | 단점 |
|---|---|---|---|
| 브루트 포스 | ‘모든 경우의 수를 탐색’하면서 원하는 결과를 얻는 알고리즘을 의미한다 | 가능한 모든 경우를 다 검사하기 때문에 예상된 결과를 얻을 수 있음 | 경우의 수가 많을 경우 시간이 오래 걸림 |
| 비트마스크 | ‘모든 경우의 수’를 이진수료 표현하고 ‘비트 연산’을 통해 원하는 결과를 빠르게 얻는 알고리즘을 의미 | 이진수 연산을 이용하여 계산 속도가 빠름 | 경우의 수가 많아질수록 메모리 사용량이 늘어남 |
| 백트래킹 | 결과를 얻기 위해 진행하는 도중에 ‘막히게 되면’ 그 지점으로 다시 돌아가서 ‘다른 경로를 탐색’하는 방식을 의미, 결국 모든 가능한 경우의 수를 탐색하여 해결책을 찾음 | 경우의 수를 줄이면서도 모든 경우를 탐색할 수 있음 | 재귀 함수를 이용하기 때문에 스택 오버플로우가 발생할 가능성 있음 |
| 순열 | ‘순열’을 이용하여 모든 경우의 수를 탐색하는 방법이다. 순열은 서로 다른 n개 중에서 r개를 선택하여 나열하는 방법을 의미 | 경우의 수가 적을 때 사용하면 유용함 | 경우의 수가 많을 경우 시간이 오래 걸림 |
| 재귀함수 | 자기 자신을 호출하여 모든 가능한 경우의 수를 체크하면서 최적의 해답을 얻는 방식을 의미 | 코드가 간결하며, 이해하기 쉬움 | 스택 오버플로우가 발생할 가능성이 있음 |
| DFS/BFS | 깊이 우선 탐색(DFS: Depth-First Search) - 루트 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법을 의미 너비 우선 탐색(Breadth-First Search: BFS) - 루트 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방법을 의미 |
미로 찾기 등에 유용함 | 최악의 경우, 모든 노드를 다 방문해야 하므로 시간이 오래 걸림 |
1. 브루트포스 - 최소 직사각형
💡 문제 설명
- 명함 지갑을 만드는 회사에서 지갑의 크기를 정하려고 한다. 다양한 모양과 크기의 명함들을 모두 수납할 수 있으면서, 작아서 들고 다니기 편한 지갑을 만들어야 한다. 이러한 요건을 만족하는 지갑을 만들기 위해 디자인팀은 모든 명함의 가로길이와 세로 길이를 조사했다. 아래 표는 4가지 명함의 가로길이와 세로 길이를 나타낸다.
- <하단의 표 1을 참고>
- 가장 긴 가로 길이와 세로 길이가 각각 80, 70이기 때문에 80(가로) x 70(세로) 크기의 지갑을 만들면 모든 명함들을 수납할 수 있다. 하지만 2번 명함을 가로로 눕혀 수납한다면 80(가로) x 50(세로) 크기의 지갑으로 모든 명함들을 수납할 수 있다. 이때의 지갑 크기는 4000(=80 x 50)이다.
- 모든 명함의 가로 길이와 세로 길이를 나타내는 2차원 배열 sizes가 매개변수로 주어진다. 모든 명함을 수납할 수 있는 가장 작은 지갑을 만들 때, 지갑의 크기를 return 하도록 solution 함수를 완성해라.
💡 제한사항
- sizes의 길이는 1 이상 10,000 이하
- sizes의 원소는 [w, h] 형식
- w는 명함의 가로 길이를 나타낸다
- h는 명함의 세로 길이를 나타낸다
- w와 h는 1 이상 1,000 이하인 자연수이.
[문제 설멍] 표1
| 명함번호 | 가로길이 | 세로길이 |
|---|---|---|
| 1 | 60 | 50 |
| 2 | 30 | 70 |
| 3 | 60 | 30 |
| 4 | 80 | 40 |
입출력 예
| sizes | result |
|---|---|
| [[60, 50], [30, 70], [60, 30], [80, 40]] | 4000 |
| [[10, 7], [12, 3], [8, 15], [14, 7], [5, 15]] | 120 |
| [[14, 4], [19, 6], [6, 16], [18, 7], [7, 11]] | 133 |
💡 해당 문제의 요점은 ‘브루트 포스’ 알고리즘을 통해 ‘카드의 사이즈를 구하기 위해서 모든 경우의 수를 다 확인’하여서 결과를 찾는다는 점이다.
- [STEP1] 2차원 배열을 1차원 배열로 분해하여 순회한다(* 카드의 모든 경우의 수를 순회)
- [STEP2] 카드의 가로와 세로의 길이 중 ‘최대값’을 구하고 이전 카드의 너비와 비교하여 ‘최대값’을 구한다.
- [STEP3] 카드의 가로와 세로의 길이 중 ‘최소값’을 구하고 이전 카드의 높이와 비교하여 ‘최대값’을 구한다.
- [STEP4] 최종적으로 계산된 너비와 높이값을 구하여 최종 카드 사이즈를 구한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static void main(String[] args) {
int answer = 0;
// int[][] size = { {60, 50}, {30, 70}, {60, 30}, {80, 40} };
// int[][] size = { {10, 7}, {12, 3}, {8, 15}, {14, 7}, {5, 15} };
int[][] size = { {14, 4}, {19, 6}, {6, 16}, {18, 7}, {7, 11} };
int width = 0; // 총 계산된 카드의 너비
int height = 0; // 총 계싼된 카드의 높이
// [STEP1] 2차원 배열을 1차원 배열로 순회한다. (* 카드의 모든 경우를 순회 )
for (int[] card : size) {
int cardItemWidth = card[0]; // n번 명함의 가로 길이
int cardItemHeight = card[1]; // n번 명함의 세로 길이
// [STEP2] 카드의 기로와 세로의 길이 중 최대 값과 이전 카드 사이즈를 비교하여 최종 너비값을 구한다.
width = Math.max(width, Math.max(cardItemWidth, cardItemHeight));
// [STEP3] 카드의 가로와 세로의 길이 총 최소 값과 이전에 카드 사이즈를 비교하여 최종 높이값을 구한다.
height = Math.max(height, Math.min(cardItemWidth, cardItemHeight));
}
// [STEP4] 최종적으로 계산된 너비와 높이 값을 곱하여 결과값을 구합니다.
answer = width * height;
System.out.println("answer : "+answer);
}
2. 브루트포스 - 모의고사
💡 문제 설명
- 수포자는 수학을 포기한 사람의 준말이다.
- 수포자 삼인방은 모의고사에 수학 문제를 전부 찍으려 한다.
- 수포자는 1번 문제부터 마지막 문제까지 다음과 같이 찍는다.
- 1번 수포자가 찍는 방식: 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, …
- 2번 수포자가 찍는 방식: 2, 1, 2, 3, 2, 4, 2, 5, 2, 1, 2, 3, 2, 4, 2, 5, …
- 3번 수포자가 찍는 방식: 3, 3, 1, 1, 2, 2, 4, 4, 5, 5, 3, 3, 1, 1, 2, 2, 4, 4, 5, 5, …
1번 문제부터 마지막 문제까지의 정답이 순서대로 들은 배열 answers가 주어졌을 때, 가장 많은 문제를 맞힌 사람이 누구인지 배열에 담아 return 하도록 solution 함수를 작성하자.
💡 제한사항
- 시험은 최대 10,000 문제로 구성되어 있고, 문제의 정답은 1, 2, 3, 4, 5중 하나이다.
- 가장 높은 점수를 받은 사람이 여럿일 경우, return 하는 값을 오름차순 정렬해라.
입출력의 예
| answers | return |
|---|---|
| [1,2,3,4,5] | [1] |
| [1,3,2,4,2] | [1,2,3] |
💡 해당 문제의 요점은 ‘브루트 포스’ 알고리즘을 통해 ‘수포자의 패턴’을 통해 결과를 얻기 위해 모든 경우의 수를 다 확인’하여서 결과를 찾는다는 점이다.
- [STEP1] 수포자들의 문제를 찍는 패턴 정의한다.
- [STEP2] 문제 배열을 순회하면서 각각의 값을 Counting 한다. (* 모든 경우의 수를 순회)
- [STEP3] 구성한 리스트의 최대값을 구한다.
- [STEP4] 최대값인 사용자를 구한다.
- [STEP5] 최종 배열로 구성.(List to Array[])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public static void main(String[] args) {
// 1번 문제부터 마지막 문제까지의 정답이 순서대로 들어있는 배열 answers
// int[] answers = new int[]{1, 2, 3, 4, 5};
int[] answers = new int[]{1, 3, 2, 4, 2};
List<Integer> personScoreList = Arrays.asList(0, 0, 0);
// [STEP1] 수포자들의 문제를 찍는 패턴 정의
int[] person1Pattern = new int[]{1, 2, 3, 4, 5};
int[] person2Pattern = new int[]{2, 1, 2, 3, 2, 4, 2, 5};
int[] person3Pattern = new int[]{3, 3, 1, 1, 2, 2, 4, 4, 5, 5};
// [STEP2] 문제 배열을 순회하면서 각각의 값을 Counting (* 모든 경우의 수를 순회)
for (int i = 0; i < answers.length; i++) {
if (answers[i] == person1Pattern[i % 5]) personScoreList.set(0, personScoreList.get(0) + 1);
if (answers[i] == person2Pattern[i % 8]) personScoreList.set(1, personScoreList.get(1) + 1);
if (answers[i] == person3Pattern[i % 10]) personScoreList.set(2, personScoreList.get(2) + 1);
}
// [STEP3] 구성한 리스트의 최대값
int max = Collections.max(personScoreList);
// [STEP4] 최대값인 사용자
List<Integer> maxPersonList = new ArrayList<>();
for (int i = 0; i < personScoreList.size(); i++) {
if (max == personScoreList.get(i)) maxPersonList.add(i + 1);
}
// [STEP5] 최종 배열로 구성 (List to Array[])
int[] answer = maxPersonList.stream().mapToInt(i -> i).toArray();
maxPersonList.stream().mapToInt(i -> i).forEach(i -> System.out.println("answer : "+i));
}
3. 비트마스크 - 비밀지도
💡 문제 설명
- 네오는 평소 프로도가 비상금을 숨겨놓는 장소를 알려줄 비밀지도를 손에 넣었다.
- 그런데 이 비밀지도는 숫자로 암호화되어 있어 위치를 확인하기 위해서는 암호를 해독해야 한다.
- 다행히 지도 암호를 해독할 방법을 적어놓은 메모도 함께 발견했다.
- 지도는 한 변의 길이가 n인 정사각형 배열 형태로, 각 칸은 “공백”(“ “) 또는 “벽”(“#”) 두 종류로 이루어져 있다.
- 전체 지도는 두 장의 지도를 겹쳐서 얻을 수 있다.(각각 “지도 1”과 “지도 2”라고 하자.)
- 지도 1 또는 지도 2 중 어느 하나라도 벽인 부분은 전체 지도에서도 벽이다.
- 지도 1과 지도 2에서 모두 공백인 부분은 전체 지도에서도 공백이다.
- “지도 1”과 “지도 2”는 각각 정수 배열로 암호화되어 있다.
- 암호화된 배열은 지도의 각 가로줄에서 벽 부분을 1, 공백 부분을 0으로 부호화했을 때 얻어지는 이진수에 해당하는 값의 배열이다.
네오가 프로도의 비상금을 손에 넣을 수 있도록, 비밀지도의 암호를 해독하는 작업을 도와줄 프로그램을 작성하라.
💡 입력 형식
- 입력으로 지도의 한 변 크기 n과 2개의 정수 배열 arr1, arr2가 들어온다.
- 1 ≦ n ≦ 16
- arr1, arr2는 길이 n인 정수 배열로 주어진다.
- 정수 배열의 각 원소 x를 이진수로 변환했을 때의 길이는 n 이하이다. 즉, 0 ≦ x ≦ 2n - 1을 만족한다.
💡 출력 형식
- 원래의 비밀지도를 해독하여 ‘#’, 공백으로 구성된 문자열 배열로 출력하라.
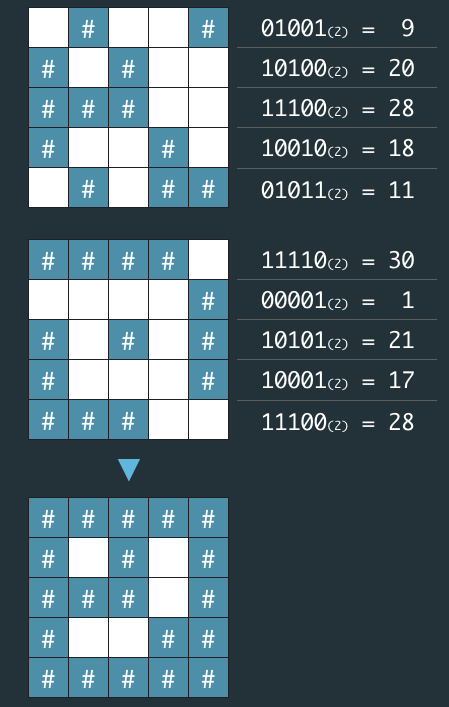
💡 입출력 예제
| 매개변수 | 값 |
|---|---|
| n | 5 |
| arr1 | [9, 20, 28, 18, 11] |
| arr2 | [30, 1, 21, 17, 28] |
| 출력 | [”#####”,”# # #”, “### #”, “# ##”, “#####”] |
| 매개변수 | 값 |
|---|---|
| n | 6 |
| arr1 | [46, 33, 33 ,22, 31, 50] |
| arr2 | [27 ,56, 19, 14, 14, 10] |
| 출력 | [”######”, “### #”, “## ##”, “ #### “, “ #####”, “### # “] |
💡 해당 문제의 요점은 ‘비트 마스크’ 알고리즘을 통해 숫자 이진수로 변환 후 연산을 통해 최종 결과값을 찾는다는 점이다.
- [STEP1] 결과 값을 넣을 배열의 사이즈를 구성
- [STEP2] arr1와 arr2의 비트 연산자로 ‘OR 연산자’ 계산을 하고 이진수로 변환한 값을 결과 배열에 넣어둔다.(비트마스크 - 이진수로 변환하여 연산)
- [STEP3] 구성한 이진수 배열을 순회하며 0인경우 “ “ 공백으로 변환하고 1인 경우 “#”으로 변환
- [STEP4] 결과값을 도출
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static void main(String[] args) {
// int n = 5;
// int[] arr1 = new int[]{9, 20, 28, 18, 11};
// int[] arr2 = new int[]{30, 1, 21, 17, 28};
int n = 6;
int[] arr1 = new int[]{46, 33, 33, 22, 31, 50};
int[] arr2 = new int[]{27, 56, 19, 14, 14, 10};
// [STEP1] 결과값을 넣을 배열의 사이즈를 구성
String[] answer = new String[n];
// [STEP2] arr1와 arr2의 비트 연산자로 'OR 연산자' 계산을 하고 이진수로 변환한 값을 결과 배열에 넣어ensek.(비트마스크 - 이진수로 변환하여 연산)
for (int i = 0; i < arr1.length; i++) {
answer[i] = Integer.toBinaryString(arr1[i] | arr2[i]);
}
// [STEP3] 구성한 이진수 배열을 순회하며 0인경우 " " 공백으로 변환하고 1인 경우 "#"으로 변환
for (int i = 0; i < answer.length; i++) {
answer[i] = String.format("%" + n + "s", answer[i]); // n 길이에 맞게 문자열을 맞춘다.
answer[i] = answer[i].replace("1", "#"); // "1"의 값인 경우 "#"로 치환
answer[i] = answer[i].replace("0", " "); // "0"의 값인 경우 " "로 치환
}
Arrays.asList(answer).forEach(i -> System.out.println("i : "+i));
}
4. 브루트포스 - 카펫
💡 문제 설명
Leo는 카펫을 사러 갔다가 아래 그림과 같이 중앙에는 노란색으로 칠해져 있고 테두리 1줄은 갈색으로 칠해져 있는 격자 모양 카펫을 봤다.
Leo는 집으로 돌아와서 아까 본 카펫의 노란색과 갈색으로 색칠된 격자의 개수는 기억했지만, 전체 카펫의 크기는 기억하지 못했다.
Leo가 본 카펫에서 갈색 격자의 수 brown, 노란색 격자의 수 yellow가 매개변수로 주어질 때 카펫의 가로, 세로 크기를 순서대로 배열에 담아 return 하도록 solution 함수를 작성하라.
💡 제한사항
- 갈색 격자의 수 brown은 8 이상 5,000 이하인 자연수이다.
- 노란색 격자의 수 yellow는 1 이상 2,000,000 이하인 자연수이다
- 카펫의 가로 길이는 세로 길이와 같거나, 세로 길이보다 길다.
💡 입출력 예제
| brown | yellow | return |
|---|---|---|
| 10 | 2 | [4, 3] |
| 8 | 1 | [3, 3] |
| 24 | 24 | [8, 6] |
💡 해당 문제의 요점은 ‘브루트 포스’ 알고리즘을 통해 역순으로 배열을 순회하면서 모든 경우의 수를 다 확인하여 결과를 찾는다는 점이다.
- [STEP1] 갈색 격자와 노란 격자를 합하여 전체의 개수를 구한다.
- [STEP2] 그 합의 제곱근부터 1이 될 때까지 반복 수행 (브루트 포스)
- [STEP3] 반복 수행을 하면서 그 중 합의 약수인 경우를 찾는다.
- [STEP4] 약수 중 합에서 가로의 길이를 나누어서 세로(j)의 길이를 계산
- [STEP5] 가로(i)와 세로(j)의 길이를 이용하여 노란색 타일의 개수가 맞는지 확인하고, 맞을 경우에는 해당 크기를 반환
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public static void main(String[] args) {
int[] answer = new int[2];
// int brown = 10;
// int yellow = 2;
// int brown = 8;
// int yellow = 1;
int brown = 24;
int yellow = 24;
// [STEP1] 갈색 격자와 노란 격자를 합하여 전체의 개수를 구합니다.
int sum = brown + yellow;
// [STEP2] 그 합의 제곱근부터 1이 될 때까지 반복 수행합니다. (브루트 포스)
for (int i = (int) Math.sqrt(sum); i >= 1; i--) {
// [STEP3] 그 중 합의 약수인 경우를 찾습니다.
if (sum % i == 0) {
// [STEP4] 약수 중 합에서 가로의 길이를 나누어서 세로의 길이를 계산합니다.
int j = sum / i;
// [STEP5] 가로와 세로의 길이를 이용하여 노란색 타일의 개수가 맞는지 확인하고, 맞을 경우에는 해당 크기를 반환합니다.
if ((i - 2) * (j - 2) == yellow) {
answer = new int[]{j, i};
}
}
}
Arrays.stream(answer).forEach(System.out::println);
}


댓글남기기